正则表达式引擎

| 阅读次数

正则表达式

这里就讨论最简单的正则表达式实现，由字符集[a-zA-Z0-9]和*，+，?，|组成。

1. NFA

正则表达式和一个不确定有限状态自动机（NFA）是等价的。可以根据一个正则表达式创建一个NFA。比如有正则表达式a(bb)+a，可以构建如下等价的NFA：

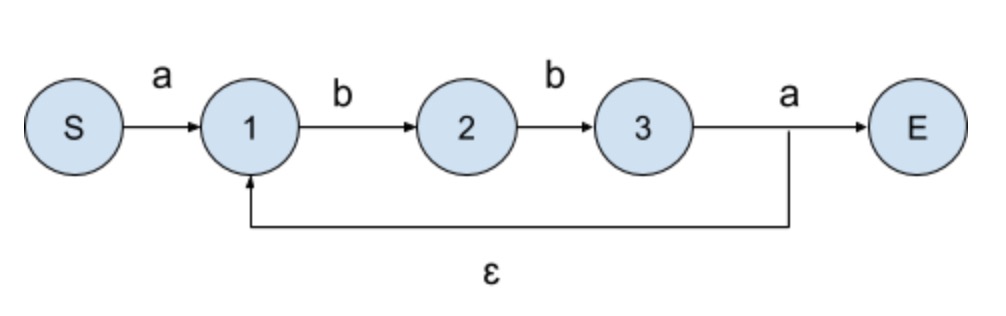
其中ɛ表示一个空字符串，即状态3可以直接跳转到状态1，或者在遇到字符a时跳转到匹配状态E。

1.1 构造NFA

要由一个正则表达式构造一个NFA，可以将正则表达式分割成由以下基本组件构成：

Concate: e1e2
Split: e1|e2
Optional: e?
Plus: e+
Star: e*

每一个基本组件对应的NFA的分别为：

Concate,

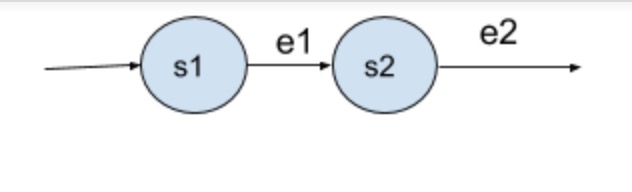
Split,

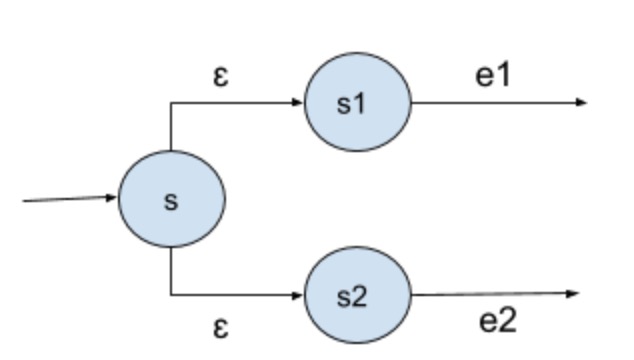
Optional

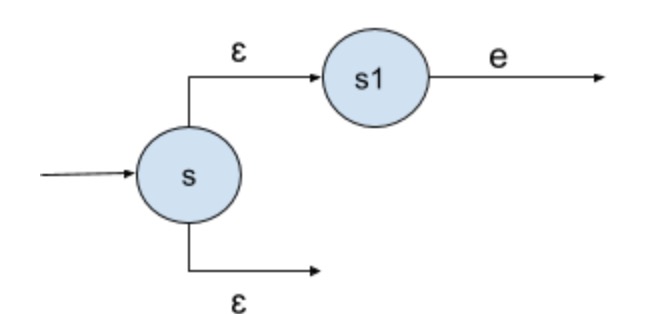
Plus,

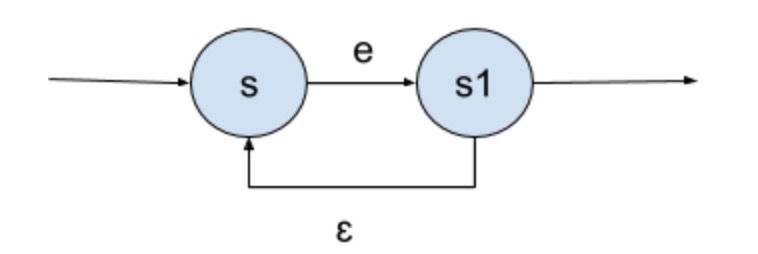
Star

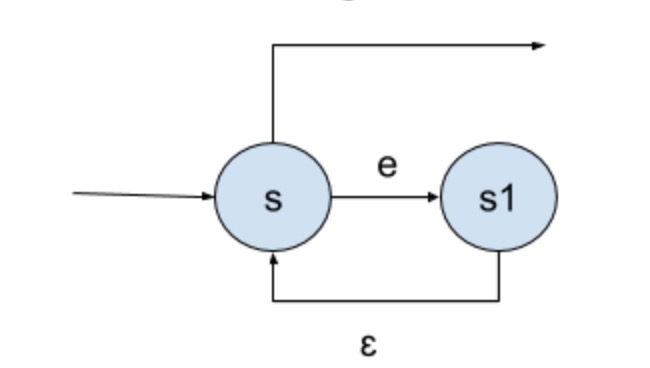
正则表达式a(bb)+a可以拆分成

1	e1 = bb e2 = e1+ e3 = ae2 e4 = e3a

这样构造出来的NFA就是文章开头的NFA

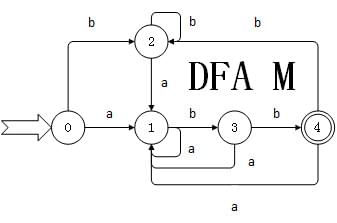
2. DFA

确定有限状态自动机（DFA）和NFA的不同之处在于DFA的每一个状态的输入和输出都只有一个，而且DFA没有ɛ边。DFA和NFA是等价的，一个NFA可以转化为一个DFA，而且所有等价的DFA最终可以转化为一个最优化的DFA。

NFA转化成DFA的关键在于找到ɛ闭包，一个状态s的ɛ闭包为s经过任意条ɛ边所能达到的状态的集合。构造DFA的过程其实就是不断计算ɛ闭包的过程。比如有下面的NFA：

构造DFA的步骤如下：

计算状态0的ɛ闭包，ɛ-closure({0}) = {0, 1, 2, 4, 7} = T0
计算T0中的所有状态在输入字符集中的一个字符时得到的状态集合，move(T0, a) = {3, 8}，move(T0, b) = {8}
分别计算结果结合的ɛ闭包，ɛ-closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} = T1， ɛ-closure({8}) = {1, 2, 4, 5, 6, 7} = T2
对T1和T2重复上述操作，直到没有新的集合产生。

这样之后{Ti}即新的DFA的状态集合，用表格记录计算结果，

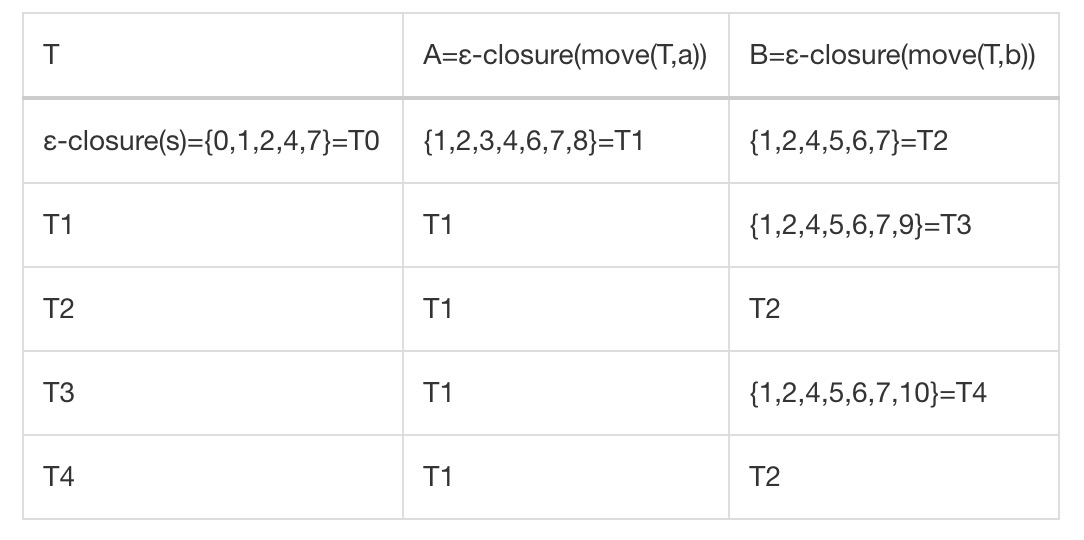
上文的NFA构造之后的DFA结果为：

Rust-Object-Safe

| 阅读次数

Rust中同时支持动态分派和静态分派。

静态分派

所谓静态分派，是指编译器就知道调用哪一个函数来实现多态。举个例子来说，我们有一个Foo Trait，并为u8和String实现了这个Trait：

trait Foo {
  method(&self) -> Stirng;
}

impl Foo for u8 {
    fn method(&self) -> String { format!("u8: {}", *self) }
}

impl Foo for String {
    fn method(&self) -> String { format!("string: {}", *self) }
}

如果我们定义如下的泛型函数

1
2
3

fn do_something<T: Foo>(x: T) {
    println!("{}", x.method());
}

并这样调用这一个泛型函数

fn main() {
  	let x = 5u8;
  	let y = "Hello".to_string();
    
    do_something(x);
    do_something(y);
}

由于在编译阶段编译器已经知道了x和y的类型，那么编译器会在调用泛型函数的时候展开函数，即编译器会生成类似下面的代码：

fn do_something_u8(x: u8) {
    x.method();
}

fn do_something_string(x: String) {
    x.method();
}

fn main() {
    let x = 5u8;
    let y = "Hello".to_string();

    do_something_u8(x);
    do_something_string(y);
}

这样一来，泛型函数的调用就变成了特定类型展开结果的内联调用，这样的优点是显而易见的：内联函数易于优化，而且快！当然，内联函数过多，代码也会变成臃肿，同时”优化“也并不见得是真的优化。

动态分派

由于静态分派有瑕疵，也就有了动态分派。动态分派是通过Trait Object实现的，Trait Object指的是类型直到运行时才能确定的对象，如&Foo，Box\等，其实也就是指向Trait的指针了。

一个Trait Object其实是一个胖指针，它的内存结构为：


pub struct TraitObject {
    pub data: *mut (),
    pub vtable: *mut (),
}

可以看到Trait Object是通过虚函数表来实现动态分派的，但是Rust的虚函数表和C++的虚函数表不同的是，在C++中，每一个对象实例中都存在一个vtable指针，而在Rust中，对象实例是没有vtable指针的，vtable阵阵存在于Trait Object中。

一个vtable实际上就是包裹了函数指针的结构，还是以Foo这个Trait为例子，一个可能的实现如下：

struct FooVtable {
  	desctructor: fn(*mut ()),
    size: usize,
    align: usize,
    method: fn(*const ()) -> String,
}
fn call_method_on_u8(x: *const()) -> String {
  	let byte: &u8 = unsafe{ &*(x as *const u8)};
    byte.method()
}

fn call_method_on_string(x: *const()) -> String {
  	let string: &String = unsafe {&*(x as *const String)};
	string.method()
}

static Foo_for_u8_vtable: FooVtable = FootVtable {
  	destructor:/* a destructor*/,
    size: 1,
    align: 1,
    method: call_method_on_u8 as fn(*const()) -> String
};
    
static Foo_for_string_vtable: FooVtable = FooVtable {
  	desctructor: /* a desctructor*/,
    size: 24,
    align: 8,
    method: call_method_on_string as fn(*const()) -> String
};

这样之后，编译器就可以把let p = &x as &Foo做如下的转换：

// let p = &x as &Foo
let p = TraitObject {
  	data: &a,
    vtable: &Foo_for_u8_vtable
};

调用Trait Object对应的方法也就转换成了：

1 2	// p.method() p.vtable.method(p.data)

Object Safe

并不是所有的Trait都可以有相应的Trait Object的，一个Trait如果想要构造出一个Trait Object，那么这个Trait必须时Object Safe的，那什么是Object Safe呢？它必须满足以下两个条件：

trait没有Self: Sized约束
trait中所有的方法都是object safe的

trait中所有的方法都是Object Safe的是指：
- 不能有任何的类型参数，即方法不能是泛型的
- 方式中没有Self参数
一个Trait 只是描述了一个类型的公共行为，它并不知道这个类型的具体实现的大小，也就是说实现这些公共行为的具体类型大小各异，并不受拘束，那么如果我们给一个Trait加上Self: Sized约束，这就是告诉我们，这个Trait所描述的具体类型大小在编译器就知道了，即它的大小是一个常量，而这与Trait Object是相违背的。所以如果我们像下面一样定义一个Trait，我们是没有办法构造出一个Trait Object的。
1
2
3
4
5
6
7
trait Foo where Self: Sized {
fn foo(&self);
}

...

// let p = &x as &Foo; // error
有时候我们只是想让某些方法不出现在vtable中，而不是构造不出Trait Object，这个时候只要给对应的方法加上Self: Sized约束即可。即:
1
2
3
4
5
6
7
8
9
10
trait Foo {
fn foo(&self);
fn not_in_vtable(&self) where Self: Sized;
}

...

let p = &x as &Foo;
p.foo(); // corrent
// p.not_in_vtable(); // error
一个trait方法如果有一个Self参数会发生什么呢？拿Clone举个例子，
1
2
3
4
5
6
7
8
9
10
pub trait Clone {
fn clone(&self) -> Self;

fn clone_from(&mut self, source: &Self) { ... }
}

...

let p = &x as &Clone;
let y = p.clone()；
首先由x得到了一个Trait Object，这个时候编译器已经不知道x原来的类型是什么了，只是只要由p可以调用一些列Clone所定义的方法，而接下来又要调用clone这个函数来复制x的一个实例，这就让编译器犯难了，即然它都不知道原先的类型是啥，又何谈复制？所以Rust就规定这种情况下，Trait不是Object Safe的，也就不能构造出Trait Object。

如果一个trait方法没有self参数，即为一个静态方法，那么很显然静态方法是没有办法放进vtable中的，所以静态方法也不是object safe的

如果trait方法中有类型参数，比如：
1
2
3
trait Foo {
fn foo<T>(&self, t: T);
}
由于泛型参数是在编译期自动展开的，如果要讲泛型函数放到vtable中，就必须把所有的foo版本都赛到虚函数表中，这个就太为难Rust编译器了，所以Rust规定，如果有类型参数，那么方法也不是Object Safe的。

Multiplicative Hashing

| 阅读次数

Multiplicative Hashing

Multiplicative Hashings是一种基于取余运算的高效哈希算法。
假设我们有一个基于链表的hash map，其伪代码结构如下：

struct HashMap {
...
private:
  array<List> elements;
...
}

令2^d = elements.size(), 那么哈希函数定义如下：

1	hash(x) = (z * x mod (2^w)) div (2^(w-d))

其中z是在{1…2^w-1}中随机选取的一个奇数且w > d.

下面给出两个定理来说明该哈希函数为什么是高效的。

定理1

1	对于任意的x, y∈{1...2^w-1}, 且x != y, 那么有 P{hash(x) == hash(y)} <= 2 / (2^d). P{t}表示t出现的概率。

定理2

1	对于任意的x，elements[hash(x)].size() <= Nx + 2, 其中Nx表示x在hash map中出现的次数。

定理的证明参见《open data structures》中HashMap一节。

Knuth Arithmetic Algorithm

| 阅读次数

Knuth Arithmetic Algorithm

大整数的四则运算的经典算法：

n位整数的加法或者减法，给出一个n位整数的答案和一个进位
n位整数和m位整数的乘法，给出一个（m+n）位的答案
（m+n）位整数除以n位整数，给出（m+1）位的商和n位的余数

记(Un-1Un-2…U0)b是为b进制下，每个位为Ui，i >= 0 &&i <= n-1的大整数。

加法算法

给定非负整数(Un-1Un-2…U0)b和(Vn-1Vn-2…V0)b，算法结果为一个b的进制整数和(WnWn-1…W0)b，这里Wn是进位，总是等于0或者1.

算法流程：

A1. 初始化。置j <- 0, k <- 0, 变量j将跑遍各个数字的位置, 而k记住在每个步骤的进位。
A2. 置Wj <- (Uj + Vj + k ) mod b，k <- (Uj + Vj + k) / b （整数除法）
A3. j <- j + 1，若j < n, 则跳转到A2，否则置Wn <- k.

减法算法

给定非负整数(Un-1Un-2…U0)b >= (Vn-1Vn-2…V0)b, 这个算法形成它们非负b进制的差(Wn-1Wn-2…W0)b.

算法流程：

1	S1. 初始化. 置 j <- 0, k <- 0 S2. 置Wj <- (Uj - Vj + k) mod b, k <- (Uj - Vj + k) / b, (整数除法). S3. j <- j + 1, 如果j < n, 则跳转到S2, 否则算法终止.

乘法算法

给定非负整数(Um-1Um-2…U0)b和(Vn-1Vn-2…V0)b, 算法形成它们的b进制乘积(Wm+n-1….W1W0)b.

算法流程：

M1. 初始化, 置Wm-1, Wm-2, ..., W0为0，j <- 0.
M2. 如果Vj = 0, 那么置Wj+m = 0, 并跳转M6
M3. 置 i <- 0, k <- 0
M4. 置 tmp <- Ui * Vj + Wi+j + k, 然后置 Wi+j <- t mod b, k <- t / b (整数除法)
M5. i <- i + 1, 如果i < m, 则跳转M4
M6. j <- j + 1, 如果j < n, 则跳转M2, 否则算法终止.

除法运算

考虑长除法，每一个步骤是(n+1)位被除数u除以n位除数v的除法，每一步之后的余数r小于v，随后的步骤中使用r*b+(被除数的下一位)作为新的u. 那么
问题就简化到对一个非负整数u = (UnUn-1…U0)b和v = (Vn-1Vn-2…V0), 求一个算法以确定q = 下取整(u/v).
这里直接给出定理，证明可以参见《计算机编程艺术》第二卷4.3.1节。
记q’ = min(下取整[(Unb + Un-1) / Vn-1], b - 1).

定理1

q’ >= q

定理2

如果Vn-1 >= 下取整(b/2), 那么q’ - 2 <= q <= q’

定理3

令r’ = (Unb + Un-1 - q’ Vn-1), 假设Vn-1 > 0, 那么如果q’Vn-2 > b r’ + Un-2, 那么 q < q’

定理4

如果q’Vn-2 <= br’ + Un-2, 那么q’ = q或者q = q’ - 1

于是我们有以下算法：
给定非负整数u = (Um+n…U1U0)b和v = (Vn-1..V1V0)b，其中Vn-1 != 0且n > 1. 构造b进制的商为(qmqm-1…q0)b和余数, (rn-1…r1r0)b.

算法流程：

D1. 规格化. 置d <- [b / (Vn-1 + 1)], 然后置u = u * d, v = v * d, 这样做事为了让Vn-1 >= b/2.
D2. 初始化. 置j <- m.
D3. 置q' <- (Uj+n * b + Uj+n-1) / Vn-1, 并令r' = Uj+n * b + Uj+n-1 - q'*Vn-1, 测试q' = b 或者q'Vn-2 > b * r' + Un-2, 如果是，
那么q' <- q' - 1, r' <- r' + Vn-1, 如果r' < b, 则重复上述测试。
D4. 以(Uj+nUj+n-1...Uj)b - q' * (Vn-1Vn-2...V0)b代替(Uj+nUj+n-1...Uj)
D5. qj <- q', 如果D4的结果为负，那么跳转到D6，否则到D7
D6. qj <- qj - 1, 把(0Vn-1Vn-2...V0)b加到(Uj+nUj+n-1...Uj)上
D7. j <- j - 1, 如果j >= 0, 跳转到D3.
D8. (qm...q1q0)即所求的商，余数则可以剩下的(Un-1...U1U0)b除以d得到

Type deduction in CPP

| 阅读次数

模板类型推导

假设我们有如下的模板函数：

1 2	template <typename T> void f(ParamType param);

一个该模板函数的调用语句可能如下所示：

f(expr);

在编译阶段，编译器利用expr来推导出两个类型：T和ParamType。ParamType常带有变量的限定符，如const和引用符号。
模板的类型推到不仅仅依赖于expr的类型，还依赖于ParamType的类型，ParamType共分为三种类型：

ParamType是一个指针或者引用（但不是universal reference, T&&)
ParamType是一个universal reference
ParamType既不是一个指针也不是一个引用
根据ParamType的类型，模板的类型推到规则也有三种。

1. ParamType是一个指针或者引用（但不是一个universal reference）

这种情况下的推导规则为：

如果expr是一个引用，那么忽略expr的引用
然后根据expr的类型和ParamType的类型，推导出T

举几个例子：

template <typename T>
void f(T& param);

int x = 27;
const int cx = x;       // cx is const int
const int& rx = x;      // rx is const int&

f(x);       // x is int => T is int, param's type is int&
f(cx);      // cx is const int => T is const int, param's is const int&
f(rx);      // rx is const int& => T is const int, param's type is const int&

template <typename T>
void f(T* param);

int x = 27;
const int *px = &x;

f(&x);      // T is int, param's type is int*
f(px);      // T is const int, param's type is const int*

2. ParamType是一个universal reference

一般来说函数模板有以下形式：

1 2	template <typename T> void f(T&& param);

param类型由以下规则得得出：

T& + T& => T&
T& + T&& => T&
T&& + T& => T&
T&& + T&& => T&&

举几个例子：

template <typename T>
void f(T&& param);

int x = 27;
const int cx = x;
const int& rx = x;

f(x);       // x is lvalue, T is int&, param's type is int&
f(cx);      // cx is lvalue, T is const int&. param's type is const int&
f(rx);      // rx is lval, T and param is const int&
f(27);      // 27 is rvalue, T is int, param's type is int&&

3. ParamType既不是指针也不是引用

一般来说函数模板有以下形式：

1 2	template <typename T> void f(T param);

此时，传递给函数的实参会被拷贝。此时函数模板的推导规则如下：

如果expr是引用，那么它的引用被忽略

之后，如果expr有const限定符，那么const被忽略，如果有volatile限定符，volatile被忽略。
还是例子：

int x = 27;
const int cx = x;
const int& rx = x;

f(x);       // T's and param's types are both int
f(cx);      // T's and param's types are both int
f(rx);      // ditto

注意到只是顶级const被忽略，如果有这样一次函数调用：

1 2	const char* const ptr = "Fun with pointers"; f(ptr);

那么在函数中修改ptr所指向的字符串是不被允许的，而修改ptr这个指针（如使其为nullptr）则是可以的。

数组参数

数组和指针是不同的类型，但是数组类型自动转换成指针类型，于是下面的代码是成立的：

1 2	const char name[] = "Test"; const char* ptrName = name;

在模板函数中，如果数组是有by-value传递给函数的，那么数组自动转换成指针，如果by-reference传递给函数，那么函数得到的是一个数组的引用。即：

template <typename T>
void f1(T param);

template <typename T>
void f2(T& param);

int arr[] = {1, 2, 3};

f1(arr);        // T is int*
f2(arr);        // T is int[], parameter's type is int (&)[]

于是我们可以用以下函数在编译期得到一个数组的大小：

template <typename T, std::size_t N>
constexpr std::size_t arraySize(T (&)[N]) noexcept {
    return N;
}

当然在C++11标准中，更推荐用std::array来使用数组

1 2	int keyVals[] = {1, 2, 3}; std::array<int, arraySize(keyVals)> anotherArray;

函数参数

函数在C++中也是一种类型，而函数指针是一个指针类型，只是函数类型可以自动转换成函数指针。在函数模板中，函数的转换规则和数组类型相同。
举几个例子：

void someFunc(int, double);

template <typename T>
void f1(T param);

template <typename T>
void f2(T& param);

f1(someFunc);       // param's type is void (*)(int, double)
f2(someFunc);       // param's type is void (&)(int, double)

auto类型推导

auto关键字是由C++11引入的，本质上auto类型推导和模板类型推导是一样的，只要把auto当作是T，而变量的类型当作是模板参数类型，等号右侧当作是expr即可。如：

auto x = 27;        // auto -> T, auto -> paramType, so x is int
const auto cx = 27;  // auto -> T, const auto -> paramType, so T is int, cx is const int
const auto& rx = x; // auto -> T, const auto& -> paramType, so T is int, rx is const int&

auto&& uref1 = x;   // x is lvalue => uref1 is int&
auto&& uref2 = cx;  // cx is lvalue => uref2 is const int&
auto&& uref3 = 28;  // 28 is rvalue => uref3 is int&&

const char name[] = "Test";

auto arr1 = name;   // arr1 is const char*
auto& arr2 = name;  // arr2 is const char (&)[5]

void someFunc(int, double);
auto func1 = someFunc;  // func1 is void (*)(int, double)
auto& func2 = someFunc; // func2 is void (&)(int, double)

唯一的不同是，对于auto，如果等号右边是大括号包围的列表，那么变量自动推导为std::initializer_list<T>，而对于模板函数，传递一个{t1, t2, ..., tn}给函数会导致编译错误。

auto t = {1, 2, 3};     // t's type is std::initializer_list<int>

template <typename T>
void f(T param);

f({1, 2, 3});       // error!

template <typename T>
void f_(std::initializer<T> il);

f_({1, 2, 3});      // correct

decltype类型推导

decltype关键字用来得到表达式的类型。给几个例子：

const int i = 0;    // decltype(i) is const int
bool f(const Widget& w);    // decltype(f) is bool(const Widget&), function type
                            // decltype(w) is const Widget&
struct Point {
    int x, y;
};                          // decltype(Point::x) is int
                            // decltype(Point::y) is int
Widget w;   // decltype(w) is Widget
if (f(w)) {...} // decltype(f(w)) is bool or can convert to bool

std::vector<int> v;     // decltype(v) is std::vector<int>

于是我们可以写出以下函数：

template <typename T, typename Index>
auto authAndAccess(Container& c, Index i) -> decltype(c[i])
{
    authUser();
    return c[i];
}

operator[]可能返回容器中的一个元素的引用或者返回容器中元素的拷贝，通过上述函数我们可以将这两种情况一同处理。
decltype有一个特殊情况需要注意，如果括号内是一个变量名，那么通常我们得到的是我们想要的类型，如果括号内是一个表达式，那么我们得到的是一个T&，即

1
2
3

int x = 0;
// decltype(x)  is int
// decltype((x)) is int&

boost::typeindex

boost中的typeindex模块可以在运行时得到正确的推导类型，一个例子如下：

#include <iostream>
#include <vector>

#include <boost/type_index.hpp>

struct Widget {
    int x;
};

template <typename T>
void f(const T& param) {
    using std::cout;
    using boost::typeindex::type_id_with_cvr;

    cout << "T =\t"
         << type_id_with_cvr<T>().pretty_name()
         << '\n';

    cout << "param =\t"
         << type_id_with_cvr<decltype(param)>().pretty_name()
         << '\n';
}

int main() {
    std::vector<Widget> vw = {{1}, {2}, {3}};
    const auto k = vw;
    f(&k[0]);
    return 0;
}

输出

1	T = Widget const* param = Widget const* const&

Websocket协议

| 阅读次数

Websocket握手

客户端握手请求

客户端发送一个正常的HTTP报文，报头信息类似为：

GET /chat HTTP/1.1
Host: example.com:8080
Upgrade: websocket
Connection: Upgrade
Sec-Websocket-Key: dGhlIHNhbXBsZSBub25jZQ==
Sec-Websocket-Protocol: chat, superchat
Sec-Websocket-Version: 13

1	Upgrade: websocket Connection: Upgrade

这两个字端告诉服务器客户端请求的是Websocket协议

1	Sec-Websocket-Key: dGhlIHNhbXBsZSBub25jZQ==

由客户端随机生成，用于验证服务端的服务器用语处理这个请求的处理是否是Websocket助理

1	Sec-Websocket-Protocol: chat, superchat

子协议，用于表明客户端期望的子协议，服务器在子协议中选择支持的协议返回给客户端

1	Sec-Websocket-Version: 13

Websocket协议版本，固定为13

服务器返回握手请求

1	HTTP/1.1 101 Switching Protocols Upgrade: websocket Connection: Upgrade Sec-Websocket-Accept: s3pPLMBiTxaQ9kYGzzhZRbK+xOo= Sec-Websocket-Protocol: chat

这里就不对服务器的响应再作叙述。

在握手完成之后客户端和服务器就可以开始发送Websocket报文了，报文以桢的形式发送，和HTTP报文再没有什么关系，报文格式参考RFC即可。

Type Conversions

| 阅读次数

Trait Object

静态分派和动态分派

Rust支持静态分派(static dispatch)和动态分派(dynamic dispatch)。

静态分配是在编译阶段就确定好了应该调用哪个函数，它是通过泛型实现的多态。一个例子如下：

trait Birt {
    fn fly(&self);
}
struct Duck;
struct Swan;

impl Bird for Duck {
  	fn fly(&self) { println!("Duck fly");}
}

impl Bird for Swan {
  	fn fly(&self) { println!("Swan fly");}
}

fn test<T: Bird>(arg: T) {
  	arg.fly()
}

上述例子就是利用泛型实现了多态，在编译阶段，编译器会根据实际调用的参数不同，直接生成不同的函数版本：

// 伪代码
fn test_Duck(arg: Duck) {
  arg.fly();
}

fn test_Swan(arg: Swan) {
  arg.fly();
}

动态分派就是调用哪个函数必须在运行时才能决定。Rust中动态分派是靠Traint Object实现的，一个Trait Object就是执行Trait的指针，如果Bird是一个Trait，那么&Bird，Box都是Trait Object。

一个指向Trait的指针是一个胖指针，它不仅包含所指向的对象的元素，也包含一个虚函数表，用以在运行时决定这个Trait Object对应的函数实现调用。Rust中一个Trait Object的内部表示如下：

pub struct TraitObject {
  	pub data: *mut (),
    pub vtable: *mut (),
}

Object Safe

Trait Object的构造受到很多约束，在约束不能满足的时候就会产生编译错误。

trait有Self:Sized约束时，不能构造Trait Object。

如：

trait Foo where Self: Sized {
  	fn foo(&self);
}

impl Foo for i32 {
  fn foo(&self) {..}
}

fn main() {
  	let x = 1_i32;
    x.foo();
    let p = &x as &Foo;	// error
    p.foo();
}

上述代码会产生编译错误。

如果Trait没有加上Self: Sized约束，而Trait中某一个某一个方法加上了Self: Sized约束，那么这个方法不会出现在Trait Object中。示例如下：

trait Foo {
    fn foo1(&self);
    fn foo2(&self) where Self:Sized;
}
impl Foo for i32 {
    fn foo1(&self) {
        println!("Foo1");
    }

    fn foo2(&self) {
        println!("Foo2");
    }
}

fn main() {
    let x = 1i32;
    x.foo2();

    let p = &x as &Foo;
    p.foo2();	// error
}

当函数中有Self类型作为参数或者返回类型时(不包括self这个参数)，不能构造Trait Object

有这样的一个例子：

pub trait Clone {
  	fn clone(&self) -> Self;
    fn clone_from(&mut self, source: &Self) {...}
}
// 伪代码
let p : &Clone = xxx;
let o = p.clone();

由于p时一个trait object，编译器只知道它是一个胖指针，包含了具体对象的指针以及指向虚函数表的指针。p指向具体的对象，它的类型是什么已经不知道了，编译器知道的只是这个对象实现了Clone这个Trait，而clone方法却要求返回一个与p指向的对象一样的类型的值，这个是无法完成的任务，所以这个Clone不是object safe的。

那么如果我们需要让一个Trait满足Object safe同时又要能够构造Trait Object该怎么办呢，还记得上面提到的Self: Sized约束吧，利用它就可以了。

trait Double {
  	fn new() -> Self where Self: Sized;
    fn double(*mut self);
}

这样之后我们就可以狗仔一个trait object了，当然这个trait object的虚函数表里不存在new这个函数。

当函数有泛型参数时，不能构造trait object

假如有这样的trait

1
2
3

trait SomeTrait {
  	fn generic_fn<A>(&self, value: A);
}

如果我们使用trait object来调用这个函数：

fn func(x: &SomeTrait) {
  	x.generic_fn("foo");
    x.generic_fn(1u8);
}

这样会有一个问题，x是一个trait object，调用它的方法时是通过vtable虚函数表来进行查找并调用的，现在要调用的函数成了泛型函数，而泛型是在编译阶段自动展开的，generic_fn函数实际上有许多不同的版本，而把这些版本都塞进去是很困难的，Rust直接禁止使用trait object来调用泛型函数。

如果有静态方法，那么这个Trait不适Object safe的。

要构造这样的Trait Object，解决方法依然是利用Self: Sized约束。

Trait Object

| 阅读次数

Trait Object

静态分派和动态分派

Rust支持静态分派(static dispatch)和动态分派(dynamic dispatch)。

静态分配是在编译阶段就确定好了应该调用哪个函数，它是通过泛型实现的多态。一个例子如下：

trait Birt {
    fn fly(&self);
}
struct Duck;
struct Swan;

impl Bird for Duck {
  	fn fly(&self) { println!("Duck fly");}
}

impl Bird for Swan {
  	fn fly(&self) { println!("Swan fly");}
}

fn test<T: Bird>(arg: T) {
  	arg.fly()
}

上述例子就是利用泛型实现了多态，在编译阶段，编译器会根据实际调用的参数不同，直接生成不同的函数版本：

// 伪代码
fn test_Duck(arg: Duck) {
  arg.fly();
}

fn test_Swan(arg: Swan) {
  arg.fly();
}

pub struct TraitObject {
  	pub data: *mut (),
    pub vtable: *mut (),
}

Object Safe

Trait Object的构造受到很多约束，在约束不能满足的时候就会产生编译错误。

trait有Self:Sized约束时，不能构造Trait Object。

如：

trait Foo where Self: Sized {
  	fn foo(&self);
}

impl Foo for i32 {
  fn foo(&self) {..}
}

fn main() {
  	let x = 1_i32;
    x.foo();
    let p = &x as &Foo;	// error
    p.foo();
}

上述代码会产生编译错误。

如果Trait没有加上Self: Sized约束，而Trait中某一个某一个方法加上了Self: Sized约束，那么这个方法不会出现在Trait Object中。示例如下：

trait Foo {
    fn foo1(&self);
    fn foo2(&self) where Self:Sized;
}
impl Foo for i32 {
    fn foo1(&self) {
        println!("Foo1");
    }

    fn foo2(&self) {
        println!("Foo2");
    }
}

fn main() {
    let x = 1i32;
    x.foo2();

    let p = &x as &Foo;
    p.foo2();	// error
}

当函数中有Self类型作为参数或者返回类型时(不包括self这个参数)，不能构造Trait Object

有这样的一个例子：

pub trait Clone {
  	fn clone(&self) -> Self;
    fn clone_from(&mut self, source: &Self) {...}
}
// 伪代码
let p : &Clone = xxx;
let o = p.clone();

那么如果我们需要让一个Trait满足Object safe同时又要能够构造Trait Object该怎么办呢，还记得上面提到的Self: Sized约束吧，利用它就可以了。

trait Double {
  	fn new() -> Self where Self: Sized;
    fn double(*mut self);
}

这样之后我们就可以狗仔一个trait object了，当然这个trait object的虚函数表里不存在new这个函数。

当函数有泛型参数时，不能构造trait object

假如有这样的trait

1
2
3

trait SomeTrait {
  	fn generic_fn<A>(&self, value: A);
}

如果我们使用trait object来调用这个函数：

fn func(x: &SomeTrait) {
  	x.generic_fn("foo");
    x.generic_fn(1u8);
}

如果有静态方法，那么这个Trait不适Object safe的。

要构造这样的Trait Object，解决方法依然是利用Self: Sized约束。

Procedural Macro

| 阅读次数

Procedural Macros

Rust提供了一个derive的机制可以很方便地生成一些代码，在Rust 1.15以前定制derive的功能只在nightly里才有，Rust 1.15把这一个功能稳定了，也就是说我们可以在stable的版本里面定制derive了。

Rust book里面有一个章节Procedural Macros简单介绍了如何编写一个derive，最后的效果如下所示：

#[macro_use]
extern crate hello_world_derive;

trait HelloWorld {
    fn hello_world(&self);
}

#[derive(HelloWorld)]
struct Test1;

#[derive(HelloWorld)]
struct Test2;

fn main() {
    // println!("Hello, world!");

    let t1 = Test1;
    let t2 = Test2;

    t1.hello_world(); // print "Hello World from Test1"
    t2.hello_world(); // print "Hello World from Test2"
}

hello_world_derive

接下来就解析一下具体的细节。

我们需要新建一个crate，这个crate里面包含自动生成代码的细节，我们将其命名为hello_world_derive。在现阶段，必须把这些实现放在另外一个crate中，不过在将来可能就不需要这么麻烦了。

新建的crate的Cargo.toml文件如下：

[package]
name = "hello_world_derive"
version = "0.1.0"
authors = ["Zach <zach_41@163.com>"]

[dependencies]
quote = "*"
syn = "*"

[lib]
proc-macro = true

proc-macro 值为true表示这是一个Procedural Macro的crate。

lib.rs里面的代码如下：

extern crate proc_macro;
extern crate syn;
#[macro_use]
extern crate quote;

use proc_macro::TokenStream;

fn impl_hello_world(ast: &syn::MacroInput) -> quote::Tokens {
    let name = &ast.ident;

    quote! {
        impl HelloWorld for #name {
            fn hello_world(&self) {
                println!("Hello World from {}!", stringify!(#name));
            }
        }
    }
}

#[proc_macro_derive(HelloWorld)]
pub fn hello_world(input: TokenStream) -> TokenStream {
    let input = input.to_string();

    let ast = syn::parse_macro_input(&input).unwrap();

    let gen = impl_hello_world(&ast);

    gen.parse().unwrap()
}

先看hello_world函数，其输入是一个TokenStream，现阶段我们只能调用to_string，将它转换成字符串，然后我们调用syn模块里面的parse函数，得到一个抽象的语法树AST(类型为MacroInput)。

在implies_hello_world中我们调用分析得到的AST，并利用quote模块里的quote宏来生成需要的代码，这样就完成了自动生成了。

这里还有一个更复杂的例子derive_new，学习它对熟悉derive机制非常有帮助。

Slice和Iterator

| 阅读次数

Contiguous regions of memory

Rust用以下三种类型来处理连续的内存：

Vec\：可变大小的堆向量数组
[T; N]：编译器确定大小的数组
[T]：用于代表连续内存的slice

一个Slice只能通过特定类型的指针来操作，指针类型为以下三种：

&[T]
&mut [T]
Box<[T]>

如果我们有一个Vec<T>变量，那么我们可以通过下面的方法得到对应的Slice：

1 2	let vec = vec![12, 3, 4]; let int_slice = &vec[..];

当然也可以直接创建一个Slice变量：

1	let str_slice: &[&str] = &["one", "two", "three"];

[T; N]

[T; N]是在编译器就确定长度的数组，有两种方式创建这种数组：

[x, y, z]
[x; N]：x被重复N次

如果数组的长度小于等于32，那么如果数组的元素类型允许（即元素类型实现了对应的Trait），那么数组自动实现以下Trait：

Clone（T: Copy）
Debug
IntoIterator（&[T; N]和&mut [T; N]实现了这个Trait）
PartialEq，PartialOrd，Ord，Eq
Hash
AsRef，AsMut
Borrow，BorrowMut
Default

之所以有长度的限制，是因为Rust不支持在数组长度上的泛型，所以就实现到了长度32为止。

Iterator

迭代器可以说在Rust中占有重要的位置，在日常编码过程中我们经常会用到迭代器。这里我只是记录几点自己看标准库文档的心得，具体使用还是请看标准库文档吧。

编写一个迭代器

编写一个迭代器很简单，我们只要实现Iterator这个Trait中的next方法就好了，其余的方法我们都可以免费获得：

struct Counter {
    count: usize,
}

impl Counter {
    fn new() -> Counter {
        Counter { count: 0 }
    }
}

impl Iterator for Counter {
    type Item = usize;

    fn next(&mut self) -> Option<usize> {
        self.count += 1;
        if self.count < 6 {
            Some(self.count)
        } else {
            None
        }
    }
}

let mut counter = Counter::new();

let x = counter.next().unwrap();
println!("{}", x);

let x = counter.next().unwrap();
println!("{}", x);

再来看一下Iterator这个Trait：

pub trait Iterator {
    type Item;
    fn next(&mut self) -> Option<Self::Item>;

    fn size_hint(&self) -> (usize, Option<usize>) { ... }
    fn count(self) -> usize { ... }
    fn last(self) -> Option<Self::Item> { ... }
    fn nth(&mut self, n: usize) -> Option<Self::Item> { ... }
    fn chain<U>(self, other: U) -> Chain<Self, U::IntoIter> where U: IntoIterator<Item=Self::Item> { ... }
    fn zip<U>(self, other: U) -> Zip<Self, U::IntoIter> where U: IntoIterator { ... }
    fn map<B, F>(self, f: F) -> Map<Self, F> where F: FnMut(Self::Item) -> B { ... }
    fn filter<P>(self, predicate: P) -> Filter<Self, P> where P: FnMut(&Self::Item) -> bool { ... }
    fn filter_map<B, F>(self, f: F) -> FilterMap<Self, F> where F: FnMut(Self::Item) -> Option<B> { ... }
    fn enumerate(self) -> Enumerate<Self> { ... }
    fn peekable(self) -> Peekable<Self> { ... }
    fn skip_while<P>(self, predicate: P) -> SkipWhile<Self, P> where P: FnMut(&Self::Item) -> bool { ... }
    fn take_while<P>(self, predicate: P) -> TakeWhile<Self, P> where P: FnMut(&Self::Item) -> bool { ... }
    fn skip(self, n: usize) -> Skip<Self> { ... }
    fn take(self, n: usize) -> Take<Self> { ... }
    fn scan<St, B, F>(self, initial_state: St, f: F) -> Scan<Self, St, F> where F: FnMut(&mut St, Self::Item) -> Option<B> { ... }
    fn flat_map<U, F>(self, f: F) -> FlatMap<Self, U, F> where F: FnMut(Self::Item) -> U, U: IntoIterator { ... }
    fn fuse(self) -> Fuse<Self> { ... }
    fn inspect<F>(self, f: F) -> Inspect<Self, F> where F: FnMut(&Self::Item) -> () { ... }
    fn by_ref(&mut self) -> &mut Self { ... }
    fn collect<B>(self) -> B where B: FromIterator<Self::Item> { ... }
    fn partition<B, F>(self, f: F) -> (B, B) where B: Default + Extend<Self::Item>, F: FnMut(&Self::Item) -> bool { ... }
    fn fold<B, F>(self, init: B, f: F) -> B where F: FnMut(B, Self::Item) -> B { ... }
    fn all<F>(&mut self, f: F) -> bool where F: FnMut(Self::Item) -> bool { ... }
    fn any<F>(&mut self, f: F) -> bool where F: FnMut(Self::Item) -> bool { ... }
    fn find<P>(&mut self, predicate: P) -> Option<Self::Item> where P: FnMut(&Self::Item) -> bool { ... }
    fn position<P>(&mut self, predicate: P) -> Option<usize> where P: FnMut(Self::Item) -> bool { ... }
    fn rposition<P>(&mut self, predicate: P) -> Option<usize> where P: FnMut(Self::Item) -> bool, Self: ExactSizeIterator + DoubleEndedIterator { ... }
    fn max(self) -> Option<Self::Item> where Self::Item: Ord { ... }
    fn min(self) -> Option<Self::Item> where Self::Item: Ord { ... }
    fn max_by_key<B, F>(self, f: F) -> Option<Self::Item> where B: Ord, F: FnMut(&Self::Item) -> B { ... }
    fn max_by<F>(self, compare: F) -> Option<Self::Item> where F: FnMut(&Self::Item, &Self::Item) -> Ordering { ... }
    fn min_by_key<B, F>(self, f: F) -> Option<Self::Item> where B: Ord, F: FnMut(&Self::Item) -> B { ... }
    fn min_by<F>(self, compare: F) -> Option<Self::Item> where F: FnMut(&Self::Item, &Self::Item) -> Ordering { ... }
    fn rev(self) -> Rev<Self> where Self: DoubleEndedIterator { ... }
    fn unzip<A, B, FromA, FromB>(self) -> (FromA, FromB) where FromA: Default + Extend<A>, FromB: Default + Extend<B>, Self: Iterator<Item=(A, B)> { ... }
    fn cloned<'a, T>(self) -> Cloned<Self> where Self: Iterator<Item=&'a T>, T: 'a + Clone { ... }
    fn cycle(self) -> Cycle<Self> where Self: Clone { ... }
    fn sum<S>(self) -> S where S: Sum<Self::Item> { ... }
    fn product<P>(self) -> P where P: Product<Self::Item> { ... }
    fn cmp<I>(self, other: I) -> Ordering where I: IntoIterator<Item=Self::Item>, Self::Item: Ord { ... }
    fn partial_cmp<I>(self, other: I) -> Option<Ordering> where I: IntoIterator, Self::Item: PartialOrd<I::Item> { ... }
    fn eq<I>(self, other: I) -> bool where I: IntoIterator, Self::Item: PartialEq<I::Item> { ... }
    fn ne<I>(self, other: I) -> bool where I: IntoIterator, Self::Item: PartialEq<I::Item> { ... }
    fn lt<I>(self, other: I) -> bool where I: IntoIterator, Self::Item: PartialOrd<I::Item> { ... }
    fn le<I>(self, other: I) -> bool where I: IntoIterator, Self::Item: PartialOrd<I::Item> { ... }
    fn gt<I>(self, other: I) -> bool where I: IntoIterator, Self::Item: PartialOrd<I::Item> { ... }
    fn ge<I>(self, other: I) -> bool where I: IntoIterator, Self::Item: PartialOrd<I::Item> { ... }
}

我们必须要实现的就只是next方法，其余的都是构建在next之上，也就是说我们可以直接使用其余的方法。

Collections to Iterator

有三种方法得到一个集合的迭代器：

iter：迭代类型为&T
iter_mut：迭代类型为&mut T
into_iter：迭代类型为T

前两个方法是Slice中定义的方法，因为一个集合是一段连续的内存，所以可以调用前面两个方法。第三个方法是TraitIntoIterator中定义的接口：

pub trait IntoIterator where Self::IntoIter::Item == Self::Item {
    type Item;
    type IntoIter: Iterator;
    fn into_iter(self) -> Self::IntoIter;
}

这里有一个地方需要注意，对于一个集合，比如说Vec<T>，我们在该变量上调用into_iter，那么迭代的对象是集合的类型，在迭代之后变量的所有权就被转移了：

let v = vec![1, 2, 3];
for x in v.into_iter() {
	x;
}
// error
// v;

但是如果是一个Slice呢，在它上面调用into_iter，迭代的对象实际上是&T：

let v = &[1, 2, 3];
for x in v.into_iter() {
    println!("{}", x);
}
// will compile
v;

这是为什么呢？我们来看一下Slice文档中关于IntoIterator这个Trait的实现说明：

1	impl<'a, T> IntoIterator for &'a [T] type Item = &'a T The type of the elements being iterated over type IntoIter = Iter<'a, T> Which kind of iterator are we turning this into?

只有一句话写在那里我们也不能很相信它，于是再来看看std::iter::Iter这结构中关于Iterator 实现的说明：

1	impl<'a, T> Iterator for Iter<'a, T> type Item = &'a T The type of the elements being iterated over. fn next(&mut self) -> Option<&'a T>

可以看到Iterator这个Trait的关联类型是&T，所以我们迭代的对象的类型实际上是&T，所以在迭代之后Slice的所有权并没有转移。